Seismic Facies Identification Challenge
[Explainer] Need extra features? Different input approach? Try Seismic Attributes!
Basically it’s a math “Instagram-Snapchat-like” filter for seismic data. There are a lot of Seismic Attributes available.
Hello All, I am Leo. A simple geophysicist.
I wrote a little colab notebook on how to get new features using seismic attributes here .
What is Seismic Attributes?
Basically it’s a math “Instagram-Snapchat-like” filter for seismic data. There are a lot of Seismic Attributes available.
Seismic interpretation is subjective. Interpreter can pick/draw facies border line wherever they want even on some part of the data that got low signal to noise ratio or no reflector can be seen at all.
So, some seismic interpreters use Seismic Attributes to ‘see the data better’.
The current method that already included:
- RMS (Root Mean Square)
- MPA (Maximum Peak Amplitude)
- GLCM (Gray-Level Co-Occurrence Matrix) :
- Mean
- STD
- Contrast
- Dissimiliarity
- Homogeneity
- ASM
- Energy
- Max
- Entropy
Hope this will give you some extra data or even insight!
One of this method is what push my models to ~0.84 F1 Score. Some say it doesn’t work, maybe because we got different approach in training the models (because some other conventional data augmentation that I use which boost my score also said that doesn’t really improve their models  )
)
I will update more methods later.
Tell me if there are some errors.
Feedback and suggestion are always welcome!

Seismic interpretation is subjective.
Interpreter can pick / draw facies border line wherever they want even on some part of the data that got low signal to noise ratio or no reflector can be seen at all.
There are some method that helps seismic interpreter to 'see the data better' when interpreting using stuff called Seismic Attributes.
What is Seismic Attributes?
Basically it's a math "instagram-snapchat-like" filter for seismic data. There are a lot of Seismic Attributes available.
I will try to update more in couple of days.
For now, let's try to use the common one for facies problems, and that is..
1. GLCM (Gray-Level Co-Occurrence Matrix)¶
GLCM is a histogram of co-occurring greyscale values at a given offset over an image.
source : https://github.com/tzm030329/GLCM/
nice slide explanation by Joe Hayes : http://web.pdx.edu/~jduh/courses/Archive/geog481w07/Students/Hayes_GreyScaleCoOccurrenceMatrix.pdf
nice paper : "Application of texture attribute analysis to 3D seismic data" by Satinder Chopra and Vladimir Alexeev
First, let's get our data.
import numpy as np
import matplotlib.pyplot as plt
import scipy
import cv2
%matplotlib inline
!wget "https://datasets.aicrowd.com/default/aicrowd-public-datasets/seamai-facies-challenge/v0.1/public/data_train.npz"
For this example, let's see the inline slice no. 580 from the training data
data=np.load('data_train.npz')['data']
data.shape
slices=data[:,:,580]
plt.rcParams['figure.figsize'] = [12, 8]
plt.imshow(slices,cmap='gray',interpolation='none')
plt.show()
Then load up the function from Fast GLCM
def rescale_linear(array, new_min, new_max):
"""Rescale an arrary linearly."""
minimum, maximum = np.min(array), np.max(array)
m = (new_max - new_min) / (maximum - minimum)
b = new_min - m * minimum
return m * array + b
def fast_glcm(img, vmin=0, vmax=255, nbit=8, kernel_size=5):
mi, ma = vmin, vmax
ks = kernel_size
h,w = img.shape
# digitize
bins = np.linspace(mi, ma+1, nbit+1)
gl1 = np.digitize(img, bins) - 1
gl2 = np.append(gl1[:,1:], gl1[:,-1:], axis=1)
# make glcm
glcm = np.zeros((nbit, nbit, h, w), dtype=np.uint8)
for i in range(nbit):
for j in range(nbit):
mask = ((gl1==i) & (gl2==j))
glcm[i,j, mask] = 1
kernel = np.ones((ks, ks), dtype=np.uint8)
for i in range(nbit):
for j in range(nbit):
glcm[i,j] = cv2.filter2D(glcm[i,j], -1, kernel)
glcm = glcm.astype(np.float32)
return glcm
def fast_glcm_mean(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm mean
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
mean = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
mean += glcm[i,j] * i / (nbit)**2
return mean
def fast_glcm_std(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm std
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
mean = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
mean += glcm[i,j] * i / (nbit)**2
std2 = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
std2 += (glcm[i,j] * i - mean)**2
std = np.sqrt(std2)
return std
def fast_glcm_contrast(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm contrast
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
cont = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
cont += glcm[i,j] * (i-j)**2
return cont
def fast_glcm_dissimilarity(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm dissimilarity
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
diss = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
diss += glcm[i,j] * np.abs(i-j)
return diss
def fast_glcm_homogeneity(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm homogeneity
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
homo = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
homo += glcm[i,j] / (1.+(i-j)**2)
return homo
def fast_glcm_ASM(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm asm, energy
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
asm = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
asm += glcm[i,j]**2
ene = np.sqrt(asm)
return asm, ene
def fast_glcm_max(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm max
'''
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
max_ = np.max(glcm, axis=(0,1))
return max_
def fast_glcm_entropy(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm entropy
'''
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
pnorm = glcm / np.sum(glcm, axis=(0,1)) + 1./ks**2
ent = np.sum(-pnorm * np.log(pnorm), axis=(0,1))
return ent
Then let's run the Fast GLCMs using their default parameters.
img = rescale_linear(slices, 0, 254).astype(int)
h,w = img.shape
mean = fast_glcm_mean(img)
std = fast_glcm_std(img)
cont = fast_glcm_contrast(img)
diss = fast_glcm_dissimilarity(img)
homo = fast_glcm_homogeneity(img)
asm, ene = fast_glcm_ASM(img)
ma = fast_glcm_max(img)
ent = fast_glcm_entropy(img)
#plt.figure(figsize=(10,4.5))
plt.rcParams['figure.figsize'] = [15, 8]
fs = 15
plt.subplot(2,5,1)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(img,cmap='gray')
plt.title('original', fontsize=fs)
plt.subplot(2,5,2)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(mean)
plt.title('mean', fontsize=fs)
plt.subplot(2,5,3)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(std)
plt.title('std', fontsize=fs)
plt.subplot(2,5,4)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(cont)
plt.title('contrast', fontsize=fs)
plt.subplot(2,5,5)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(diss)
plt.title('dissimilarity', fontsize=fs)
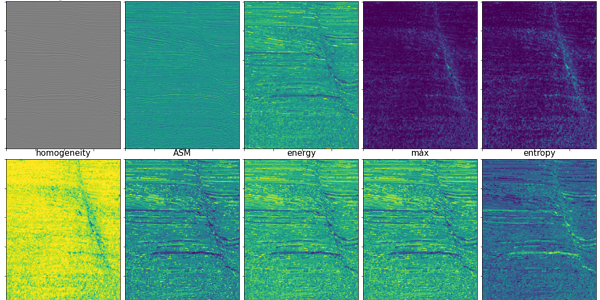
plt.subplot(2,5,6)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(homo)
plt.title('homogeneity', fontsize=fs)
plt.subplot(2,5,7)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(asm)
plt.title('ASM', fontsize=fs)
plt.subplot(2,5,8)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(ene)
plt.title('energy', fontsize=fs)
plt.subplot(2,5,9)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(ma)
plt.title('max', fontsize=fs)
plt.subplot(2,5,10)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(ent)
plt.title('entropy', fontsize=fs)
plt.tight_layout(pad=0.5)
#plt.savefig('img/output.jpg')
plt.show()
2. RMS (Root Mean Square)¶
RMS amplitude is usually for identifying reservoir properties and startigraphic events. It is the square root of the average of the amplitude sum in a window (Root Mean Square).
y=slices.shape[0]
x=slices.shape[1]
slicerms=slices.copy()*0.0
window=7
for i in range(0,x):
for j in range(0,y-7):
slicerms[j,i]=np.sqrt(np.sum(slices[j:j+window,i])**2)
plt.imshow(slicerms,cmap='RdBu',interpolation='none')
plt.show()
3. MPA (Maximum Peak Amplitude)¶
slicempa=slices.copy()*0.0
window=7
for i in range(0,x):
for j in range(0,y-7):
slicempa[j,i]=np.max(slices[j:j+window,i])
plt.imshow(slicempa,cmap='RdBu',interpolation='none')
plt.show()
Enjoy your new features to play with! :)
Content
Comments
You must login before you can post a comment.



Are you planning on releasing your code after the contest is over? I will do so, and it seems that our approaches are absolutely different, pretty much orthogonal, so it would be amazing to look at one another’s work!
I am currently considering implementing coherency with a certain window so that the reflector packages (similarly behaving reflectors) get bunched up in some big blanks on the image. This would clearly miss out on the sand channels that have small developments on the seismic cube, but should enhance the definition of big chunks of facies. I’ve seen @sergeytsimfer colab (amazing work btw) on how the NN should be able to detect and learn the ‘augmentation’ provided by seismic attributes, but does this really stand when you’re changing the image radically? Does it stand when you are stacking these different ‘augmentations’ in different channels? I’ve seen a small improvement when using the seismic attributes, but can’t really say it is a confirmed improvement since I didn’t keep working on them (trying to get the model right first). I believe this is a nice discussion to have! I’d love to see your work on coherency @sergeytsimfer .
@leocd are you using an image approach or an ndarray approach? (Maybe a ‘too soon’ question though lol)
I’ve tried following several approaches. Assuming that we have K attributes, we can either:
The first one is more general, the second requires less computational resources. In either case, it is possible for NN to learn those augmentations; but that requires data, and it can be the case that adding those features can indeed be helpful.
Also, there are some coherency functions in my colab notebook; to use them during training process, one should pre-convert the whole cube and use the stored data as it is way more effecient than computing coherency on the fly
probably, if I manage to make it readable lol.
It’s probably more to learn from yours a lot than you can learn from mine haha…
I’m trying to put everything there at first, but like @sergeytsimfer said in his notebook, it looks great visually, but some just didn’t work. So I just try it one by one to see which one that works. The rest is just augmentation (conventional and some new method) and tuning some knobs.
Your idea seems interesting I might try that as well.
I might try that as well.
I currently tinker some stuff from spectral area, but I think it won’t deliver that much.
But hey, we are working with black box system, simple data augmentation that I skipped because I think it won’t work theoretically is one of the method that push my score